MMT-ODES Working Models — II
Published on
Contents
Preparing for a mmm-0.3 model, with Godley Tables, I wanted to also take a breif excursion into fetching empirical data, specifically for New Zealand, since I do not see much point i =n making the effort to model the banking operations without some realistic empirical inputs.
This turns out to be painful, since NZ does not have a nice facility like the St Louuis FED. In fact at presetn I get some betetr quality NZ data from the FRED.
Refinement–0.3
Issue 1. We’d rather not write an arbitrary Investment function, right? The level of investment should be determined by the interest rates. But in a government centred economy — like every nation today — the interest rate is a policy parameter. So we can just look-it-up from the RBNZ or FRED or wherever. The banker only needs a credit-worthy customer. This is good for us, it means we do not need to solve some awful market equilibrium problem.
Issue 2. While I think the Two-Sector model is worth refining, and is a good one to use, it does not reveal much about the all important aspects of a nominal “democracy”, which is the Firm vs Worker conflict. It is a vitally nasty bit of the present neoliberal capitalist system. Bosses do not need to work to eat, Workers do. So,
The labour market is an unfair game.
One might even say grossly unfair, and it is not even a game, it is life & death stuff. Hence important to model you might think?
I do so think.
Unfortunately, the painfulness of model complexity starts to rare its ugly time-sucking head. I need Godley Tables at this stage if for no other reason that to avoid $\pm$ sign mistakes. But also to ensure stock-flow consistency.
Our Model is now (Three+1)-Sector Model (sounds a bit Minkowski! Have we gone relativistic?), but still closed, or if you prefer:
Workers = All workers domestic and foreign, but wages in NZD.
Firms = All firms domestic and foreign, dealing in NZD.
Government = NZ Government.
Banks = agents of the state, but still in the Godley Tables.
So the Bank sector is the “+1”.
This way we do not need to worry about imports and exports, they are taken into account.
Although our Government does not explicitly insure all bank deposits, they have a track record in propping up commercial banks, so for all intents and purposes the banks are in the Government Sector, which is why I’d call this a (3+1) model.
Investment (3+1) Sectors
The investment function can now be more complicated. We considered split private debt + loans. If we had two sectors suffering different interest rates they would just split the term into Loan and Debts, $$ \begin{align*} \mathcal{I}(\pi, D) & = \mathcal{I}(\pi) - i_d D + i_g D_g\\ \text{into},\qquad \mathcal{I} &= \mathcal{I}(\pi) - i_L F_L - i_d F_D + i_g D_g \\ \end{align*} $$ where $F_L$ are the Firm loans, and $F_D$ are the Firm debts. But this would very soon almost necessitate introducing Godley Tables to keep the loan and debt ledgers balanced, which means banking. I want to delay this modelling for now, so we will bookmark it as something to do.
As before, $D_g$ is government debt, so is the interest-earning asset of the Firms and Workers now. Though I was not sure if all of $D_g$ should go to Investment. Probably we should split this using a savings propensity, $s_g$. Then, $$ \begin{align*} \Delta \mathcal{I} &\sim (1 -s_g) i_g D_g \\ \Delta S &\sim s_g i_G D_g \end{align*} $$ and so, $$ \mathcal{I}(\pi, D_g) = \mathcal{I}(\pi) - i_L F_L - i_d F_D + (1-s_g) i_gD_g $$
OK, but this means we have to put $s_gi_GD_g$ somewhere else. Obviously in Firm and Worker deposits, $F_D$, $W_D$. But how much of the share? Should we just use the monopoly parameter $\sigma$ from before? Or add another knob to twiddle? Well, this depends on thee size of the firm I guess, so it will require a new parameter. But is is something we should have empirical data to guide us.
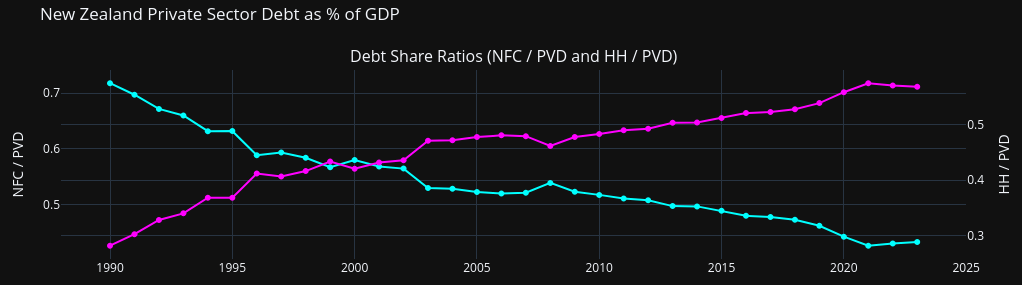
From the IMF datamapper we can get $D_g$ and the interest paid on $D_g$. But not the sector breakdown, for which we might need to dig into RBNZ data. But in lieu of that, there is a split of all “private debt, loans and securities”. That might include Tsy securities, I am not sure, but the indicator or ratio aught to be a fair proxy for the share of government interest-income.
| Year | Debt, loans, securities | % GDP |
|---|---|---|
| 2023 | Private | 161.32 |
| Household | 91.61 | |
| Nonfinancial | 60.71 |
Let’s conjure up a symbol for this ratio, say $$ \sigma_G = 0.37 $$ for “share of government interest-income (to firms)”.
Note: I will need to automate downloading these indicators. They are our “weather data”. I have not fetched from the IMF before. But is seems a simple API, just a URL that gets a JSON file, instructions here . For the indicator codes see: https://www.imf.org/external/datamapper/api/v1/indicators
TODO:
Automate these downloads (annual cron job).
# "Total stock of loans and debt securities issued by households and nonfinancial corporations as a share of GDP."
https://www.imf.org/external/datamapper/api/v1//PVD_LS/NZL
# "Total stock of loans and debt securities issued by households as a share of GDP."
https://www.imf.org/external/datamapper/api/v1//HH_LS/NZL
Since the IMF table is two years behind, but the variation smooth, I think a simple cubic spline extrapolation is ok.
The ratio has changed over time:
Other Deposit and Loan Data (could be good)
Let’s not clog up this chapter. I have another chapter on how to get some NZ economic data. A few series we will like are bank deposits, loans, and money aggregates. The RBNZ publishes these as xls spreadsheets. I will write some python scripts for retrieving these, which I will test over on the data chapter .
There are lots of nice looking series there, like Consumption (M2 table) and Investment (M3 table), and M9=labour market. M5=GDP. For our Godley Tables: bank liabilities=S40, which used to be C17 before 2017 I think? and the bank assets=S34 used to be S9.
Justifying No Foreign Sector
As regards impact on the NZ economy, we are only concerned with NZ$. But all trade balances can be converted to NZD, and New Zealand operates a floating exchange rate. So we care not about foreign flows of finance. They are part of the NZ economy at large.
What we Lose?
With this Three+1 model we cannot model the impact of foreign capital flows
on the government policy and price level. This is a major flaw in the event
of a foreign monopolist marking-up their price, especially today Crude Oil.
OK, but we’d have to manually adjust the Foreign Import price variable anyway, it’s not a market reaction function easily modelled. Thus I’m going to put off modelling the Foreign Sector and the exchange rate entirely until much later on.
Also, note we do not have a single exchange rate, the NZD floats with respect to all currencies. So this external sector modelling truly is a nightmare. It’s just worth noting what analysis we lose as a result.
- No response to forex movements.
- No response to import prices, especially crude oil.
- No response to capital flows. So we will have to try to capture such variables in some other fashion, by using empirical data, just like the Meteorological Office uses weather balloon and satellite data as inputs to revise weather forecasts.
One way to kludge this is to have an arbitrary factor adjustment in the price level that does an “all-in-one” adjustment to all three above factors. Supposing we do this by just looking at the CPI, or PCE, then our model would be empirical and would be only “good” to a few weeks out.
Government Debt
To model government bonds, or $D_g$ we could simplify a bit, since we really only need to increase the effects of $i_B$ and $i_g$ to an equivalent effective $i^\ast_B$=interest on bank deposits. What I mean is,
$i_B^\ast\cdot (F_D + W_D)$ is functionally the same as $i_B\cdot(F_D+W_D) + i_g\cdot D_g$.
This is an extreme form of what Mosler says: banks are agents of the State.
This is because it is functionally the same whenever the government insures bank deposits, which maybe despite neoliberal threats, is typically the case these days post-GFC. The government bond is only different in that it gets booked as “Government Debt” rather than Bank Liabilities. In a stable country like NZ there is a legal and psychological difference, but no practical difference (except in behavioural response functions, which of course do matter, but we will not worry since we have no clue what the behaviours will be, yet).
The psychological difference is that government bonds are considered more secure, less risky. All the risk is at the margins for traders, and who cares for them? Not me. They’re not the people feuling the real economy. ()Actually we might care, since they are the parasites. But I will care later.)
TODO
Use my PDFLaTeX notes.
I think that’s it, I think, for mmm_0_3. Try and see if it compiles and runs.
Exercise: Have a think about the need for a Foreign Sector? Is there a need?
Hint: The MMT lens is perfectly good for “highly macro”, meaning we can have Two Sector Balance, just Government and Non-Government. What is the loss in using a Two Sector model?
Reflections: In MMT unemployment is defined by:
(Unemployment) People seeking to exchange their labour or goods for tax credits.
But wat… that means we do not need a Foreign Sector. Foreigners needing our government scorepoints are unemployed in our currency, which is a waste of human lives (or at least some sort of dopiness needing elimination — maybe the Aussies borrowed some NZD off us, for whatever silly reason).
Unemployment of NZ dollars is pointless, so we can really regard foreigners as part of our economy, they are “Kiwis who do not live in NZ and do not own NZ things.” You can add, “… and who do not pay NZ taxes.” Big deal, whoop-dee-doo.
What’s the downside then?
Obviously we will not have any iodea about international fincial flows, and FOREX and sop forth can be a source of parasitic wasteful human activity, so it might be nice to use a Three Sector model. But if we are not too worried about those flows, then we should not care.
Running the Simulation
TODO
MMM-1.0 — Slightly More Monetary
The next job is the modify mmm_0_3 to include an explicit Foreign Sector
and a Job Guarantee. Maybe I will go for the JG first. The Job Guarantee
is the superior automatic stabilizer. We want to understand that this is
indeed “as advertised”.
If not? Well, then either our model is bad, or our model is good but the JG does not function as advertised. That’d be important to know!
I see it as a model test. You may not? As a model test the JG works by pure logic, so if our model does not produce an automatic stabilizer effect then our model will be wrong, and will need debugging.
Once we have confidence in the model, then the last task (for this course of study) will be to compare policies, like full JG versus full UBI.
Getting to Pro Models
Just a quick note on what to do if you are a salaried professional, but have no experience in building ODES models.
- Take the Toy model and add whatever features you think necessary for more realism, which will not be computational no-gos; and remove bits of the model you think are superfluous.
- Fetch relevant real world data for the government of interest. My minimum set currently is: (1) Unemployment (U6); (2) wage share; (3) output, (4) price level (CPI is only a rough approximant). Then we need the policy parameters: (5) interest rates (at least two); (6) tax rate (effective average).
- Use parameter fitting tools, like Monte Carlo nonlinear regressions to get fits to your other model parameters and structural constants.
- Needless to say, if you fitting was for 2023-Q1 data, then your testing needs to be for 2024-Q1, and then your forecasting can be made for 2025-Q1.
Time Periods
I have no idea yet, but I think it’d be unwise to run an MMT model for more than a quarter of the next year. But the idea would be the model has all four quarterly parameter adjustments. So we’d be able to in a single run integrate the ODE for 12 months. Any longer is mere policy analysis (the “what if’s”), not not forecasting.
Fetching Data
The USA is the best studied case, since the FRED have all the empirical data you would need to get a nice fit. Maybe also the EU as a whole? Maybe also the UK? But I have not looked into other nations. Fetching time series from the OECD and BIS portals can be automated, just not as smoothly as with the FRED.
For NZ I could not find good Treasury Statements except form the NZ Treasury XLS spreadsheets. StatsNZ is too cumbersome, and does not have the Treasury data in any convenient form I can find.
If you want to develop some neural net predictors in parallel with ODES models then banking sector data can be useful, but again our RBNZ does not have a seamless portal for fetching this data from what I can tell.
Part of the problem here is that I am only doing this as an unpaid volunteer, working “for the community” (I am my own boss, and I raise my pay by 100% every year). If some pro time were devoted to the effort then perhaps we could build a nice MMT data portal for NZ.
| Previous chapter | Back to | Next chapter |
| MMT ODE Models — I | TOC | (TBD) |
 Ōhanga Pai
Ōhanga Pai